机器学习分类算法
发表于|更新于
|字数总计:3.5k|阅读时长:14分钟|阅读量:
介绍最早以算法方式描述的分类机器学习算法:感知器和自适应线性神经元。同时我们也会使用Python来实现一个感知器。
早期机器学习概述
罗森布拉特基于MCP模型提出了第一个感知器学习法则。在这个感知器规则中,他提出了一个自学习算法,此算法通过优化得到权重系数,此系数和输入值的乘机决定了神经元是否被激活。在监督学习中,类似算法可以用于预测样本所属的类别。
我们将类别问题看作是二值分类问题,为了简单起见,分为1(正类别)和**-1(负类别)。同时定义一个激励函数$ \phi(z) $,这个函数将会以特定的输入值x和相应的权值向量w**的线性组合作为输入,也就是说:$ z=w_1x_1 + \cdots + w_nx_n $。此时定义法治函数为阶跃函数:
$$
\begin{equation}
\phi(z)=
\begin{cases}
1, & z \ge \theta \
-1, & z \lt \theta
\end{cases}
\end{equation}
$$
其中,我们称$\theta$是阈值。
为了简单起见,可以将阈值移动到等式的左边,同时初始权重是$w_0=-\theta$同时$x_0=1$,这样激励函数就变为
$$
\begin{equation}
\phi(z)=
\begin{cases}
1, & z \ge 0 \
-1, & z \lt 0
\end{cases}
\end{equation}
$$
同时感知器最初的规则很简单,可以归纳为如下几步:
- 将权重初始化为零或者一个极小的随机数。
- 迭代所有训练样本$x^i$,执行如下操作:
- 计算输出值$\hat{y}$。
- 更新权值。
每次对权重向量$w$的更新方式为:
$$
w_j:=w_j+\Delta{w_j}
$$
而对于$\Delta{w_j}$,可以通过感知器的学习规划计算获得:
$$
\Delta{w_j}=\eta(y^i-\hat{y^i})x_j^i
$$
其中,$\eta$是学习速率,一个在0到1之间的常数,$y^i$是第i个样本的真实样标,$\hat{y^i}$是相应的预测值。对于一个二维数据,可以得到如下更新公式:
$$
\Delta{w_0} = \eta(y^i-\hat{output^i})\
\Delta{w_1} = \eta(y^i-\hat{output^i})x_1^i\
\cdots
$$
需要注意的是,感知器收敛的前提是两个类别必须是线性可分的,并且学习速率足够小。
感应器的模型如下:
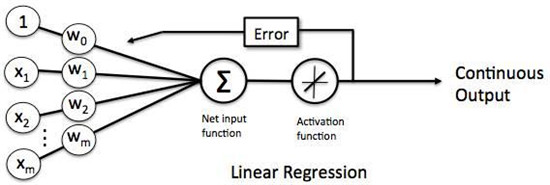
使用Python实现感知器学习算法
使用面向对象的方法实现感知器的接口,同时按照Python开发惯例,对于那些并非在初始化对象时创建但是又被对象中其他方法调用的属性,可以在后面加上一个下划线,如self.w_。
Python算法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| import numpy as np
class Perceptron(object):
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
return np.dot(X, self.w[1:]) + self.w_[0]
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, -1)
|
接下来就可以使用相关的数据集来训练我们的感知器模型。
首先我们从pandas库直接从UCI机器学习库中将鸢尾花数据集转化为DataFrame对象并且加载到内存中,并且使用tail方法显示数据确保数据加载正确。
1
2
3
4
| import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
df.tail()
|
|
0 |
1 |
2 |
3 |
4 |
| 145 |
6.7 |
3.0 |
5.2 |
2.3 |
Iris-virginica |
| 146 |
6.3 |
2.5 |
5.0 |
1.9 |
Iris-virginica |
| 147 |
6.5 |
3.0 |
5.2 |
2.0 |
Iris-virginica |
| 148 |
6.2 |
3.4 |
5.4 |
2.3 |
Iris-virginica |
| 149 |
5.9 |
3.0 |
5.1 |
1.8 |
Iris-virginica |
鸢尾花数据集时机器学习中一个经典的实例,它包含了Setosa,Versicolor和Virginica三个品种总共150个鸢尾花的测量数据,每个品种的数量是50个。每个数据项包括序号,萼片长度,萼片宽度,花瓣长度,花瓣宽度,类标。
接下来提取前100个类标,其中分别包含50个山鸢尾类标和50个变色鸢尾类标,并且将变色鸢尾表示为1,山鸢尾表示为-1。同时提取萼片长度和花瓣长度作为输入变量$X$。
首先可视化$X$:
1
2
3
4
5
6
7
8
9
10
11
12
| import matplotlib.pyplot as plt
import numpy as np
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values
plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.legend(loc='upper left')
plt.show()
|
可视化的图形如下:

现在,我们可以使用提取出的数据来训练我们的感知器了。同时我们还会绘制每次迭代的错误分类数量的折线图,以检验算法是否收敛并且找到决策边界。
1
2
3
4
5
6
| ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of misclassifications')
plt.show()
|
得到的每次迭代的错误数量折线图如下:

如上图所示,我们的迭代器在第六次的时候就已经收敛,下面通过一个简单的函数实现二维数据决策边界的可视化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
|
接着调用该函数就可以画出图像:
1
2
3
4
5
| plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()
|

通过图中可看出来,感知器能够对训练集中的所有数据进行正确的分类。
自适应线性神经元和学习的收敛性
在感知器算法出现之后,又有人提出了Adaline算法,这个算法可以看作是对之前算法的改进。
基于Adaline规则的权重更新是通过一个连续的线性激励函数来完成的,而不像感知器中使用单位阶跃函数,这是二者主要的区别。在Adaline是算法中,激励函数是简单的恒等函数,即$ \phi(w^Tx)=w^Tx $。线性激励函数在更新权重的同时,我们使用量化器对类标进行预测,量化器和前面提到的单位阶跃函数类似,如下图所示:
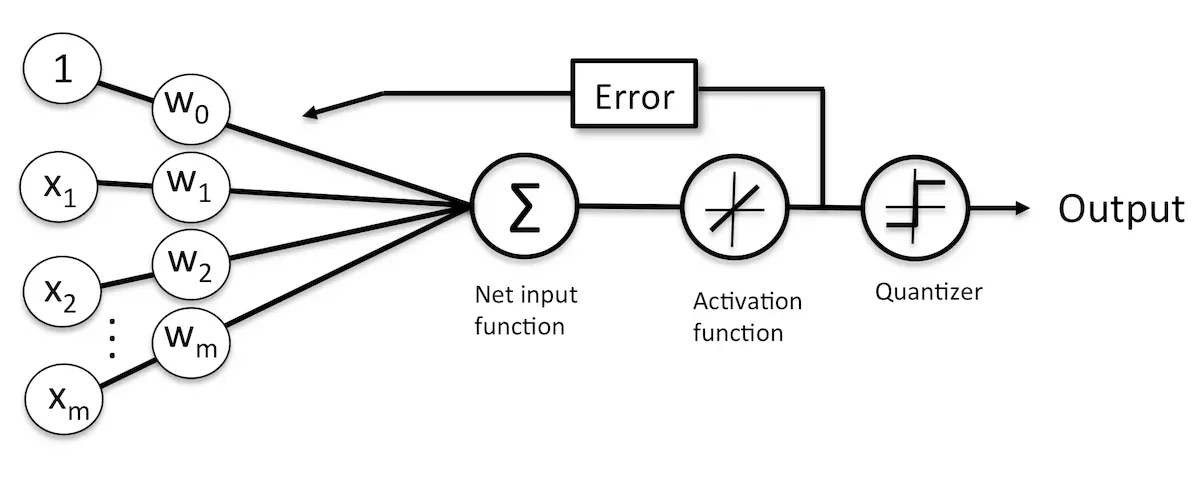
对比前面的感知器算法模型而可以得到差别:使用线性激励函数的连续型输出值,而不是二类别分类类标来计算模型的误差以及更新权重。
通过梯度下降最小化代价函数
在Adaline中,我们可以定义代价函数$J$为通过模型得到的输出值和实际值之间的误差平方和:
$$
J(w) = \frac{1}{2}\sum_i(y^i-\phi(z^i))^2
$$
这里,系数1/2是为了方便的角度,是我们容易求梯度。这个代价函数是一个凸函数,这样我们可以通过简单高效的梯度下降优化算法得到权重,并且保证对训练数据进行分类时代价最小。
如下图所示,我们将梯度学习的原理形象地描述为下山:
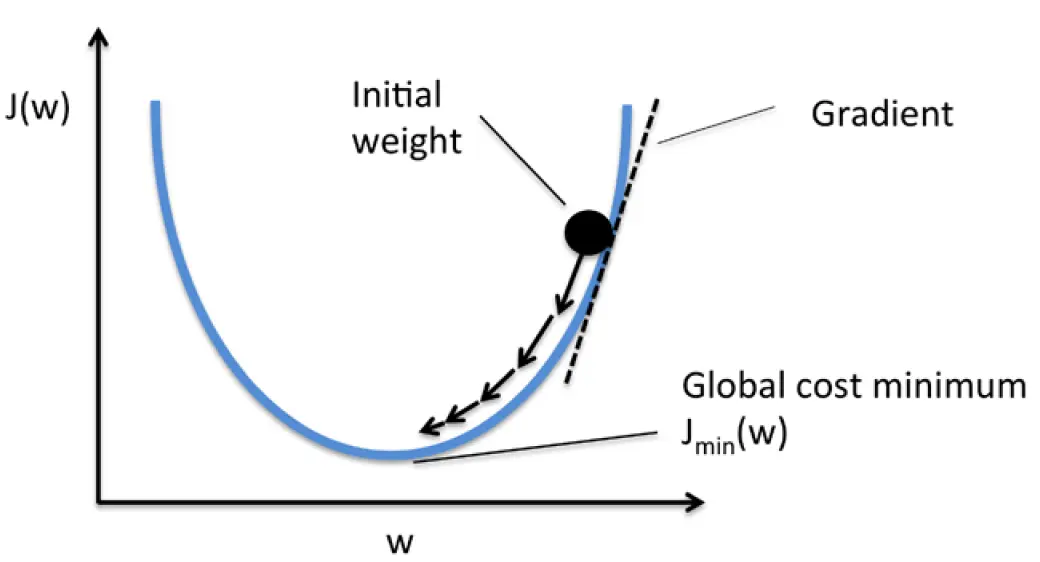
这样,权重更新公式如下:
$$
w:=w+\Delta{w}
$$
对应的权重增量$ \Delta{w} $定义为下:
$$
\Delta{w}=-\eta\Delta{J(w)}
$$
化简得到:
$$
\Delta{w_j} = \eta\sum_i(y^i-\phi(z^i))x^i_j
$$
这样权重的更行是根据训练集中所有数据完成的,而不是每次一个样本渐进更新权重,这也是该方法被称为批量下降的原因。
使用Python实现自适应线性神经元
我们将会根据感知器模型的代码来复写我们的Adaline模型,如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class AdalineGD(object):
def __init__(self, eta=0.01, n_iter=50):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum()/2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
return self.net_input(X)
def predict(self, X):
return np.where(self.activation(X) >= 0.0, 1, -1)
|
感知器通过self.eta * errors.sum()来更新第0个位置的权重,通过self.eta * X.T.dot(errors)来更新第1到m个位置的权重,同时,我们设置一个列表self.cost_用于追踪本轮训练的误差值。
实践中,我们常常需要进行调参的工作,我们分别让$\eta = 0.1$和$\eta = 0.0001$来训练,同时绘制迭代次数和代价函数的图像,观察Adaline通过数据训练进行学习的效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8,4))
ada1 = AdalineGD(n_iter=10, eta=0.1).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(SSE)')
ax[0].set_title('Adaline - 0.1')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('log(SSE)')
ax[1].set_title('Adaline - 0.0001')
plt.show()
|
图像如下:

从图中可以看出,我们面临着这两种问题:左边图像显示了学习速率过大可能会导致并没有使得代价函数尽可能低,反而因为算法跳过了全局最优解,导致误差越来越大;右边图像虽然代价函数逐渐减少,但是学习速率太小,使得到算法收敛的目标需要更多次数的迭代。
为了提高算法优化的性能,我们将使用特征缩放的方法,也就是:
$$
x_j^{‘}=\frac{x_j - \mu_j}{\sigma_j}
$$
标准化可以通过Numpy的mean和std方法实现:
1
2
3
| X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
|
接下来,按照$\eta = 0.01$的学习速率来对Adaline进行训练:
1
2
3
4
5
6
7
8
9
10
11
12
| ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - 0.01')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('SSE')
plt.show()
|
得到的图像如下:


如上图,虽然所有样本都被正确分类,但是误差平方和(SSE)的值仍然不为零。
大规模机器学习和随机梯度下降
上一节中,我们对所有的数据进行计算,利用计算出来的结果来实现权重的更新。但是,机器学习面临的数据往往是包含着几百万数据的巨大数据集,这种情况下使用批量梯度下降的计算成本很高。
为了解决这个问题,我们引入随机梯度下降,和基于所有样本的累计误差更新权重的策略不同,我们每次使用一个训练样本渐进地更新权重:
$$
\eta(y^i-\phi(z^i))x^i
$$
当实现梯度随即下降时,通常规定学习速率如下:
$$
\eta = \frac{c_1}{c_2 + [迭代次数]}
$$
为了让随机梯度下降得到更加准确的结果,让数据以随机的方式提供给算法时很重要的,因此,我们需要在每次迭代的时候打乱训练集。
随机梯度下降的另外一个优势是我们可以将其用于在线学习。通过在线学习,当有新的数据输入时模型会被实时训练。
小批次学习:介于梯度下降和随机梯度下降之间的一种技术。将数据分成一组组的训练数据,在对每组数进行训练。
随机梯度下降的Adaline算法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| from numpy.random import seed
class AdalineSGD(object):
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
if random_state:
seed(random_state)
def fit(self, X, y):
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X, y)
cost = []
for xi, target in zip(X, y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost) / len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X, y):
self._update_weights(xi, target)
else:
self._update_weights(X, y)
return self
def _shuffle(self, X, y):
r = np.random.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
self.w_ = np.zeros(1 + m)
self.w_initialized = True
def _update_weights(self, xi, target):
output = self.net_input(xi)
errors = (target - output)
self.w_[1:] += self.eta * xi.dot(errors)
self.w_[0] += self.eta * errors
cost = 0.5 * errors**2
return cost
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
return self.net_input(X)
def predict(self, X):
return np.where(self.activation(X) >= 0.0, 1, -1)
|
绘图程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
| ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - 0.01')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.show()
|
图像如下:


可以发现,代价函数的均值下降得很快,经过15次迭代后,基本趋势和梯度下降得到的图像类似。
如果改进模型,如用于数据流的在线学习,可以对单个样本简单调用partial_fit方法,如:ada.partial_fit(X_std[0, :], y[0])。










