使用回归分析预测连续型目标变量

本章将会介绍监督学习的另外一个分支，回归分析（regression analysis）。回归模型可以用于连续型目标变量的预测分析，这使得它在探寻变量间关系，评估趋势，做出预测等领域极具吸引力。具体的例子如预测公司在未来几个月的销售情况等。

简单线性回归模型初探

简单（单变量）线性回归的目标是：通过模型来描述某一特征（解释变量x）与输出变量（目标变量y）之间的关系。当只有一个解释变量时，线性模型函数定义如下：
$$
y = w_0 + w_1x
$$
其中，$ w_0 $为函数在y轴上的截距，$ w_1 $为解释变量的系数。

基于前面定义的线性方程，线性回归可以看作是求解样本点的最佳拟合直线，如下图：

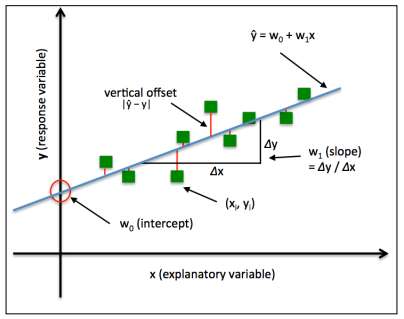
这条最佳拟合线称作是回归线，回归线和样本点之间的垂直连线就是偏移或残差。

多元线性回归函数定义如下：
$$
y = w_0x_0+w_1x_1+\cdots+w_mx_m
$$
其中，$ w_0 $时$ x_0 =1 $时在y轴上的截距。

波士顿房屋数据集

在本章的后续内容中，我们将会使用房屋价格（MEDV）作为目标变量，使用其他13个变量中的一个或多个值作为解释变量对其进行预测：

import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data', header=None, sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 
              'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()

输出如下：

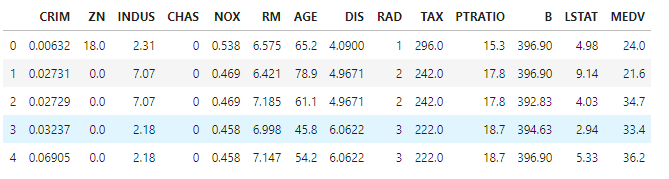
搜索性数据分析（EDA）是机器学习模型训练前的一个重要步骤。首先，借助散点图矩阵，我们可以以可视化的方法汇总显示各不同特征两两之间的关系：

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid', context='notebook')
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], size=2.5)
plt.show()

得到的图像如下：

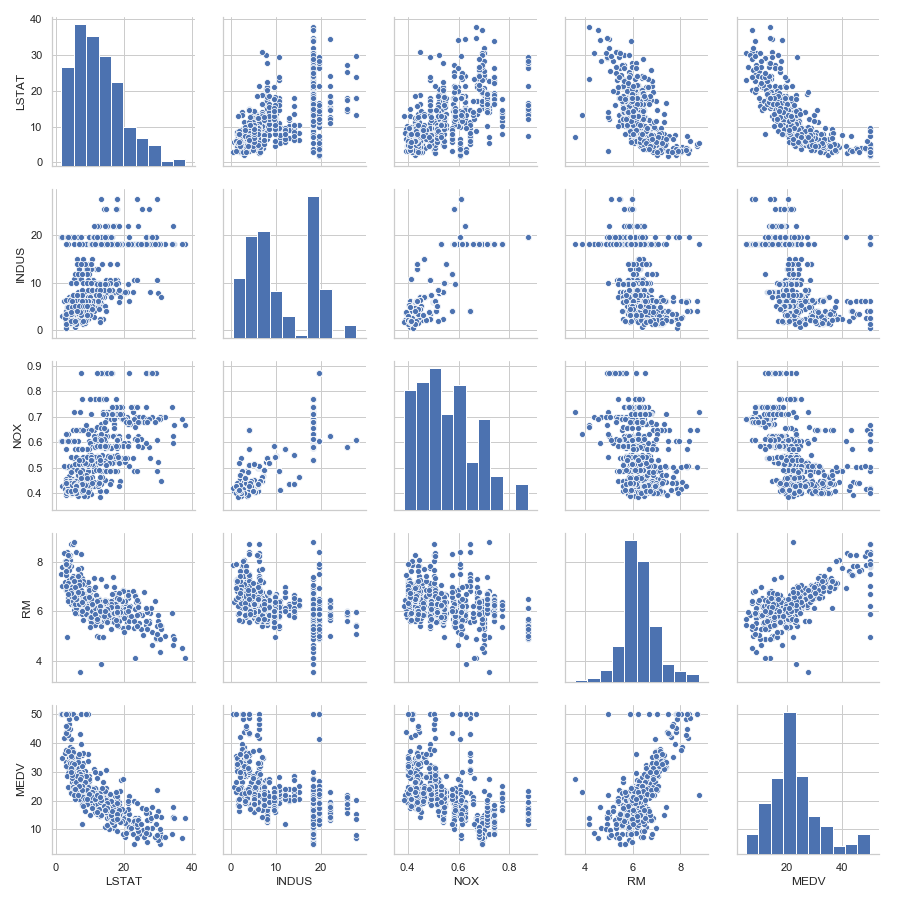
通过此散点图矩阵，我们可以快速了解数据是如何分布的，以及其中是否包含异常值。从右下角子图可以发现：MEDV看似呈正态分布，但是包含几个异常值。

为了量化特征之间的关系，我们创建一个相关系数矩阵。相关系数矩阵是一个包含皮尔逊积矩相关系数，它是用来衡量两两特征间的线性依赖关系。计算公式如下：
$$
r = \frac{\sum_{i=1}^{n}[(x^i - \mu_x)(y^i-\mu_y)]}{\sqrt{\sum_{i=1}^n(x^i-\mu_x)^2}\sqrt{\sum_{i=1}^n(y^i-\mu_y)^2}}=
\frac{\sigma_{xy}}{\sigma_x\sigma_y}
$$
其中，$ \mu $为样本特征的均值，$ \sigma_{xy} $为相应的协方差，$ \sigma_x,\sigma_y $分别为两个特征的标准差。

通过以下代码，我们计算前5个特征间的相关系数矩阵：

import numpy as np

cm = np.corrcoef(df[cols].values.T)
# sns.set(font_scale=1.5)
hm = sns.heatmap(cm, 
                cbar=True,
                annot=True,
                square=True,
                fmt='.2f',
                annot_kws={'size': 15},
                yticklabels=cols,
                xticklabels=cols)
hm.set_ylim([5, 0])
plt.show()

得到的图像如下：

为了拟合线性回归模型，我们主要关注那些跟目标变量MEDV高度相关的特征。观察前面的相关系数矩阵，可以发现MEDV与变量LSTAT的相关性最大（-0.74）。另一方面，RM和MEDV间的相关性也较高（0.70）。

基于最小二乘法构建线性回归模型

接下来我们需要对最优拟合做出判断，在此使用最小二乘法（Ordinary Least Square，OLS）估计回归曲线的参数，使得回归曲线到样本点垂直距离的平方和最小。

通过梯度下降计算回归参数

在第二章中介绍的Adaline中使用了一个线性激励函数，同时定义了一个激励函数，可以通过梯度下降（GD），随机梯度下降（SGD）等优化算法使得代价函数最小，从而得到相应的权重。Adaline中的代价函数就是误差平方和（SSE），他等同于我们定义的OLS代价函数：
$$
J(w) = \frac{1}{2}\sum_{i=1}^n(y^i - \hat{y^i})^2
$$
本质上，OLS线性回归可以理解为无单位阶跃函数的Adaline，这样我们的得到的是连续型的输出值，而不是-1或者1的类标。接下来可以看一下线性回归梯度下降代码：

class LinearRegressionGD(object):
    
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta
        self.n_iter = n_iter
    
    def fit(self, X, y):
        self.w_  = np.zeros(1 + X.shape[1])
        self.cost_ = []
        
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] +=self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.cost_.append(cost)
        return self
    
    def net_input(self, X):
        return np.dot(X, self.w_[1:] + self.w_[0])
    
    def predict(self, X):
        return self.net_input(X)

接下来我们使用房屋数据集中的RM（房间数量）作为解释变量来训练模型以预测MEDV（房屋价格）。此外，为了使得梯度下降算法收敛性更佳，在此对相关变量做了标准化处理：

X = df[['RM']].values
y = df['MEDV'].values
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
lr = LinearRegressionGD()
lr.fit(X_std, y_std)

接下来看一下代价函数和迭代次数的图像：

plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.show()

得到的图像如下：

接下来，绘制房间数和房屋价格的关系：

def lin_regplot(X, y, model):
    plt.scatter(X, y, c='b')
    plt.plot(X, model.predict(X), color='r')
    return None
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average Number')
plt.ylabel('Price')
plt.show()

得到的图像如下：

从图中可知，随着房间数的增加，房价呈现上涨趋势。但是从图中可以看到，房间数在很多的情况下并不能很好解释房价。对于经过标准化处理的变量，它们的截距必定是0：

print('Slope: %.3f' % lr.w_[1])
print('Intercept: %.3f' % lr.w_[0])

使用scikit-learn估计回归模型的系数

下面，我们使用scikit-learn中的库实现回归分析：

from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)
>> Slope: 9.102
>> Intercept: -34.671

执行代码发现得到了不同的模型系数，现在绘制出图像：

lin_regplot(X, y, slr)
plt.xlabel('Average Number')
plt.ylabel('Price')
plt.show()

得到的图像如下：

从图中可以看出，总体结果与GD算法实现的模型是一致的。

使用RANSAC拟合高鲁棒性回归模型

作为清除异常值的一种高鲁棒性回归方法，在此我们将学习随机抽样一致性（RANSAC）算法，使用数据的一个子集来进行回归模型的拟合。该算法流程如下：

1. 从数据集中随机抽取样本构建内点集合类拟合模型
2. 使用剩余数据对上一步得到的模型进行测试，并将落在预定公差范围内的样本点增至内带你集合中
3. 使用全部内点集合数据再次进行模型的拟合
4. 使用内点集合来估计模型的误差
5. 如果模型性能达到了特定阈值或者迭代达到了预定次数，则算法中止，否则跳转到第1步

首先我们用RANSACRegressor对象来实现我们的线性模型：

from sklearn.linear_model import RANSACRegressor
from sklearn.linear_model import LinearRegression
ransac = RANSACRegressor(LinearRegression(),
                        max_trials=100,
                        min_samples=50,
                        residual_threshold=5.0,
                        random_state=0)
ransac.fit(X, y)

完成拟合后，我们接着来绘制内点和异常值图像：

inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(3, 10, 1)
line_y_ransac = ransac.predict(line_X[:, np.newaxis])
plt.scatter(X[inlier_mask], y[inlier_mask], c='b', marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask], c='r', marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='g')
plt.xlabel('Average Number')
plt.ylabel('Price')
plt.legend()
plt.show()

图像如下：

接下来看一下模型的截距和斜率：

print('Slope: %.3f' % ransac.estimator_.coef_[0])
print('Intercept: %.3f' % ransac.estimator_.intercept_)
>> Slope: 10.735
>> Intercept: -44.089

线性回归模型性能的评估

现在我们使用数据集中的所有变量训练多元回归模型：

from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)

使用如下代码，我们会绘制出残差图：

plt.scatter(y_train_pred, y_train_pred - y_train, c='b', marker='o', label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test, c='r', marker='s', label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend()
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.show()

得到的残差图如下：

完美的预测结果其残差为0，但是在实际的应用中，这种情况不会出现。不过，对于一个好的回归模型，我们期望误差是随机分布在中心线附近的。

另外一种对模型性能进行定量评估的方法是均方误差（Mean Squared Error，MSE），计算公式如下：
$$
MSE = \frac{1}{n}\sum_{i=1}^{n}(y^i - \hat{y^i})^2
$$
执行如下代码：

from sklearn.metrics import mean_squared_error
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
>> MSE train: 19.958, test: 27.196

从结果而知，训练集上的MSE值为19.96，测试集上的MSE值骤升为27.20，这意味着我们的模型过拟合于训练数据。

某些情况下也可以使用决定系数来进行评估，它的计算公式如下：
$$
R^2 = 1 - \frac{MSE}{Var(y)}
$$
可以使用如下代码来计算$ R^2 $：

from sklearn.metrics import r2_score
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
>> R^2 train: 0.765, test: 0.673

回归中的正则化方法

正则化是通过在模型中加入额外信息来解决过拟合问题的一种方法，引入罚项增加了模型的复杂度但却降低了模型了模型参数的影响。最常见的正则化线性回归方法就是所谓的岭回归（Ridge Regression），最小绝对收缩及算子选择（LASSO）以及弹性网络（Elastic Net）。

岭回归是基于L2罚项的模型，我们只是在最小二乘代价函数中加入了权重的平方和：
$$
J(w){Ridge} = \sum{i=1}^{n}(y^i-\hat{y^i})^2+\lambda||w||^2_2
$$
其中：
$$
L2： \lambda||w||^2_2=\lambda\sum_{j=1}^{m}w_j^2
$$
对于稀疏数据训练的模型，还可以使用LASSO：
$$
J(w){LASSO}= = \sum{i=1}^{n}(y^i-\hat{y^i})^2+\lambda||w||1
$$
其中：
$$
L1： \lambda||w||1 = \lambda\sum{j=1}^{m}|w_j|
$$
弹性网络如下：
$$
J(w){ElasticNet} = \sum_{i=1}^{n}(y^i-\hat{y^i})^2+
\lambda_1\sum_{j=1}^{m}w_j^2+
\lambda_2\sum_{j=1}^{m}|w_j|
$$
scikit-learn中岭回归模型的初始化方法如下：

from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)

正则化强度通过alpha参数来调节，类似于参数$ \lambda $。

LASSO对象的初始化如下：

from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)

最后，scikit-learn下面的ElasticNet允许我们调整L1与L2的比率：

from sklearn.linear_model import ElasticNet
lasso = ElasticNet(alpha=1.0, l1_ratio=0.5)

线性回归模型的曲线化—-多项式回归

对于不符合线性假设的问题，一种常用的解释方法就是：
$$
y = w_0+w_1x+w_2x^2+\cdots+w_dx^d
$$
接下来我们讨论一下如何使用scikit-learn中的PolynomialFeatures转化类在只含有一个解释变量的简单回归问题中加入二次项。步骤如下：

1. 增加一个二次多项式：

   from sklearn.preprocessing import PolynomialFeatures
   X = np.array([ 258.0, 270.0, 294.0, 320.0, 342.0,
               368.0, 396.0, 446.0, 480.0, 586.0])[:, np.newaxis]
   y = np.array([ 236.4, 234.4, 252.8, 298.6, 314.2, 342.2, 360.8, 368.0, 391.2, 390.8])
   lr = LinearRegression()
   pr = LinearRegression()
   quadratic = PolynomialFeatures(degree=2)
   X_quad = quadratic.fit_transform(X)

2. 拟合一个用于对比的简单线性回归模型：

   lr.fit(X, y)
   X_fit = np.arange(250, 600, 10)[:, np.newaxis]
   y_lin_fit = lr.predict(X_fit)

3. 使用经过转换后的特征针对多项式回归拟合一个多元线性回归模型：

   pr.fit(X_quad, y)
   y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
   plt.scatter(X, y, label='training points')
   plt.plot(X_fit, y_lin_fit, label='linear fit', linestyle='--')
   plt.plot(X_fit, y_quad_fit, label='quadratic fit')
   plt.legend(loc='upper left')
   plt.show()

   得到的图像如下：

   

   从图像可以看出，和线性拟合相比，多项式拟合可以更好地捕捉到解释变量和响应变量之间的关系。

y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('Training MSE linear: %.3f, quadratic: %.3f' % (
        mean_squared_error(y, y_lin_pred),
        mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (
        r2_score(y, y_lin_pred),
        r2_score(y, y_quad_pred)))
>> Training MSE linear: 569.780, quadratic: 61.330
>> Training R^2 linear: 0.832, quadratic: 0.982        

执行上述代码后，MSE的值由线性拟合的570下降到了61。同时和线性拟合结果相比，二次模型的判定系数结果更好，说明二次拟合的效果更好。

房屋数据中的非线性关系建模

接下来，我们将会使用二次核三次多项式对房屋价格核LSTAT之间的关系进行建模，并且和线性拟合进行对比：

X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()

# create polynomial features
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)

# linear fit
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))

# quadratic fit
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))

# cubic fit
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))

# plot results
plt.scatter(X, y, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit, label='linear(d=1), R^2 = %.2f' % linear_r2, color='b', lw=2, linestyle=':')
plt.plot(X_fit, y_quad_fit, label='quadratic(d=2), R^2 = %.2f' % quadratic_r2, color='g', lw=2, linestyle='-')
plt.plot(X_fit, y_cubic_fit, label='cubic(d=3), R^2 = %.2f' % cubic_r2, color='r', lw=2, linestyle='--')
plt.xlabel('LSTAT')
plt.ylabel('Price')
plt.legend()
plt.show()

图像如下：

从图像而知，相较于线性拟合和二次拟合，三次拟合更好地捕获了房屋价格与LSTAT之间的关系。不过，加入越来越多的多项式特征会增加模型复杂度，容易造成过拟合。

此外，多项式特征并非总是非线性关系建模的最佳选择。例如，我们仅就MEDV-LSTAT的散点图来说，我们可以将LSTAT特征变量的对数值以及MEDV的平方根映射到一个特征空间，并用线性回归进行拟合：

# transform features
X_log = np.log(X)
y_sqrt = np.sqrt(y)

# fit features
X_fit = np.arange(X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]
regr = regr.fit(X_log, y_sqrt)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))

# plot results
plt.scatter(X_log, y_sqrt, label='training points',color='lightgray')
plt.plot(X_fit, y_lin_fit, label='linear(d=1), R^2=%.2f' % linear_r2, color='blue', lw=2)
plt.xlabel('LSTAT')
plt.ylabel('Price')
plt.legend()
plt.show()

得到的图像如下：

从$ R^2 $的值可以看出，这种拟合形式优于前面的任何一种多项式回归。

使用随机森林处理非线性关系

本节中，我们将会学习随机森林回归，他从概念上异于本章中介绍的其他回归模型。随机森林是多颗决策树的集合，它可以被理解成分段线性函数的集成。

1. 决策树回归

   决策树算法的一个优点是我们无需对数据进行特征转换。在scikit-learn中对其进行建模：

   from sklearn.tree import DecisionTreeRegressor
   X = df[['LSTAT']].values
   y = df['MEDV'].values
   tree = DecisionTreeRegressor(max_depth=3)
   tree.fit(X, y)
   sort_idx = X.flatten().argsort()
   lin_regplot(X[sort_idx], y[sort_idx], tree)
   plt.xlabel('LSTAT')
   plt.ylabel('Price')
   plt.show()

   图像如下：

   

   在此例中，深度为3的树看起来是比较合适的。

2. 随机森林回归

   随机森林算法是组合多颗决策树的一种集成技术。随机森林的一个优势是：它对数据集中的异常值不敏感，且无需过多的参数调优。接下来使用scikit-learn中的库来拟合一个随机森林回归模型：

   X = df.iloc[:, :-1].values
   y = df['MEDV'].values
   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
   from sklearn.ensemble import RandomForestRegressor
   forest = RandomForestRegressor(n_estimators=1000, criterion='mse', random_state=1, n_jobs=-1)
   forest.fit(X_train, y_train)
   y_train_pred = forest.predict(X_train)
   y_test_pred = forest.predict(X_test)
   print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
   print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
   >> MSE train: 1.641, test: 11.056
   >> R^2 train: 0.979, test: 0.878

   遗憾的是，我们发现随机森林对于训练数据有些过拟合，接下来看一下预测的残差图：

   plt.scatter(y_train_pred, y_train_pred - y_train, c='black', marker='o', s=35, alpha=0.5, label='Training data')
   plt.scatter(y_test_pred, y_test_pred - y_test, c='lightgreen', marker='s', s=35, alpha=0.7, label='Test data')
   plt.xlabel('Predicted values')
   plt.ylabel('Residuals')
   plt.legend()
   plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
   plt.xlim([-10, 50])
   plt.show()

   图像如下：

   

   可以发现，随机森林的残差图相比线性拟合产生的残差图有了很大的改进。