实现多层人工神经网络

本章中，我们将会学习人工神经网络的基本概念以帮助我们学习后面几章中的内容。

使用人工神经网络对复杂函数建模

我们在第二章中从人工神经元入手，开始了机器学习算法的探索。对于本章中将要讨论的多层人工神经网络来说，人工神经元是其构建的基石。

单层神经网络回顾

先来回顾一下自适应线性神经元（Adaline）算法：

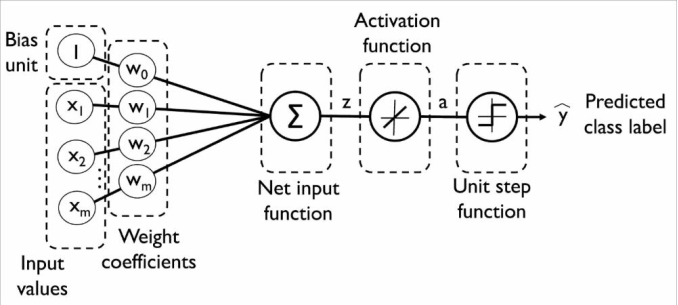
我们实现了二分类类别的Adaline算法，并通过梯度下降优化算法来学习模型的权重系数：
$$
w:=w+\Delta w,其中\Delta w = -\eta \nabla J(w)
$$
在梯度下降优化过程中，我们在每次迭代后同时更新所有权重。此外，将激励函数定义为：
$$
\phi(z)=z=a
$$
其中，净输入z时输入和权重的线性组合，使用激励函数来计算梯度更新时，我们定义了一个阈值函数将连续的输出值转换为二类别分类的预测类标：
$$
\hat{y}=\begin{cases}
1 & 若g(z) \ge 0\
-1 & 其他
\end{cases}
$$

多层神经网络架构简介

本节中，我们将会看到如何将多个单独的神经元连接为一个多层前反馈神经网络。这种特殊的网络也被称作是多层感知器（MLP）。MLP的示例图如下：

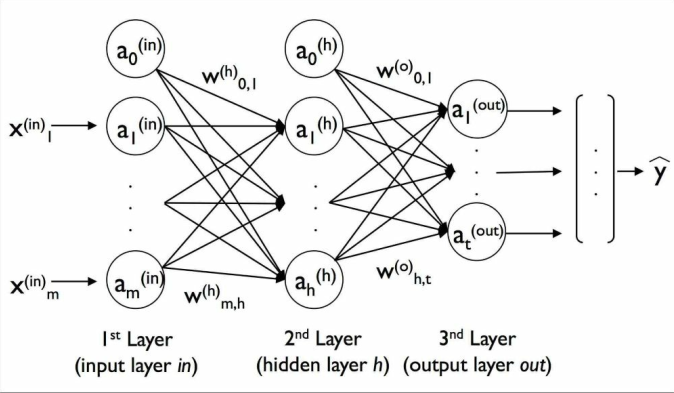
MLP包含一个输入层，一个隐层以及一个输出层。如果这样的网络中包含不只一个隐层，我们称其为深度神经网络。如图所示，我们将第l层中第i个激励单元记作$ a_i^l $，同时我们将激励单元$ a_0^{in} $和$ a_0^{h} $为偏置单元（bias unit），我们均设定为1。输入层各单元的激励为输入加上偏置单元：
$$
a^{in} = \begin{bmatrix}
a^{in}_0 \
a^{in}_1 \
\vdots \
a^{in}m
\end{bmatrix}
$$
对于第l层的各单元，均通过一个权重系数连接到$ l+1 $层中的所有单元上。如连接第l层中第k个单元与第$ l+1 $层中第j个单元的连接可记为$ w{j,k}^l $。下图是一个3-4-3多层感知器：

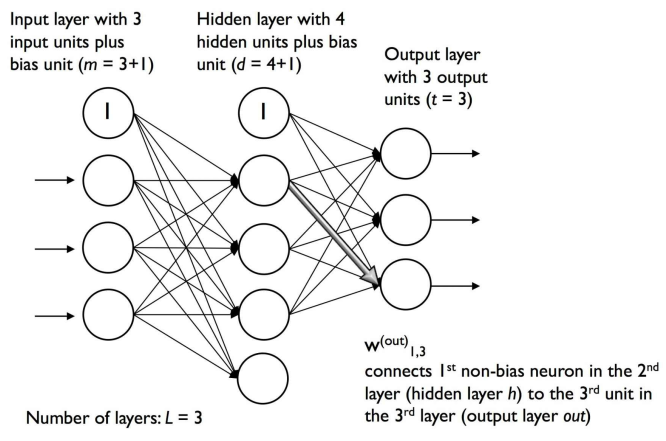
通过正向传播构造神经网络

本节中，我们将使用正向传播来计算多层感知器（MLP）模型的输出。我们将多层感知器的学习过程总结为三个步骤：

1. 从输入层开始，通过网络向前传播（也就是正向传播）训练数据中的模式，以生成输出
2. 基于网络的输出，通过一个代价函数计算所需最小化的误差
3. 反向传播误差，计算其对于网络中每个权重的导数，并且更新模型

最终通过多层感知器模型权重的多次迭代和学习，我们使用正向传播来计算输出，并使用阈值函数获得独热法所表示的预测类标。

现在，我们根据正向传播算法逐步从训练数据的模式中生成一个输出。由于隐层每个节点均完全连接到所有输入层节点，我们首先通过以下公式计算$ a_1^2 $的激励：
$$
z_1^2 = a_0^1w_{1,0}^1+a_1^1w_{1,1}^1+\cdots+a_m^1w_{1,m}^1\
a_1^2 = \phi(z_1^2)
$$
激励函数可以使用sigmoid激励函数以解决图像分类等复杂问题。

多层感知器是一个典型的前馈人工神经网络，此处的前馈指的是每一层的输出都直接作为下一层的输入。为了提高代码的执行效率和可读性，我们将使用线性代数中的基本概念：
$$
Z^2 = W^1[A^1]^T
$$
接下来我们可以将激励函数$ \phi(\cdot) $应用于净输入矩阵中的每个值，便于获取下一个激励矩阵$ A^2 $:
$$
A^2 = \phi(Z^2)
$$
类似地，我们以向量的形式重写输入层的激励：
$$
Z^3 = W^2A^2
$$
最后，通过sigmoid激励函数，我们可以得到神经网络的连续型输出：
$$
A^3 = \phi(Z^3)
$$

手写数字的识别

接下来我们看一下神经网络在实际中的应用，通过MNIST数据集上对手写数字的识别，来完成我们第一个多层神经网络的训练。MNIST是机器学习算法中常用的一个基准数据集。

获取MNIST数据集

MNIST数据集可以通过链接http://yann.lecun.com/exdb/mnist/下载，包含下列四个部分：

• 训练集图像：train-images-idx3-ubyte.gz
• 训练集类标：train-labels-idx1-ubyte.gz
• 测试集图像：t10k-images-idx3-ubyte.gz
• 测试集类标：t10k-labels-idx1-ubyte.gz

下载完数据后并解压，接下来将其读入数组并且用于训练感知器模型：

import os
import struct
import numpy as np

def load_mnist(path, kind='train'):
    labels_path = os.path.join(path, '%s-labels-idx1-ubyte' % kind)
    images_path = os.path.join(path, '%s-images-idx3-ubyte' % kind)
    with open(labels_path, 'rb') as lbpath:
        magic, c = struct.unpack('>II', lbpath.read(8))
        labels = np.fromfile(lbpath, dtype=np.uint8)
    with open(images_path, 'rb') as imgpath:
        magic, num, rows, cols = struct.unpack('>IIII', imgpath.read(16))
        images = np.fromfile(imgpath, dtype=np.uint8).reshape(len(labels), 784)
    return images, labels

load_mnist函数返回值返回两个数组，第一个是$ n\times m $维NumPy数组（存储图像），返回的第二个数组（类标）包含对应的目标变量，也即手写数字对应的类标，struct.unpack函数中的fmt参数的实参值：>II。>这是表示大端字节序，I表示一个无符号整数。

接下来我们读取数据：

X_train, y_train = load_mnist('mnist', kind='train')
print('Rows: %d, columns: %d' % (X_train.shape[0], X_train.shape[1]))
X_test, y_test = load_mnist('mnist', kind='t10k')
print('Rows: %d, columns: %d' % (X_test.shape[0], X_test.shape[1]))
>> Rows: 60000, columns: 784
>> Rows: 10000, columns: 784

为了解MNIST数据集中图像的样子，我们可以将特征矩阵中的784像素向量还原为$ 28 \times 28 $图像：

import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(10):
    img = X_train[y_train==i][0].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

图像如下：

此外，我们绘制一下相同数字的多个示例：

fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(25):
    img = X_train[y_train==7][i].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

图像如下：

实现一个多层感知器

接下来，我们实现一个包含一个输入层，一个隐层和一个输出层的多层感知器，并且将其用来识别MNIST数据集中的图像，整体代码如下：

import numpy as np
import sys

class NeuralNetMLP(object):
    def __init__(self, n_hidden=30, l2=0., epochs=100, eta=0.001,
                shuffle=True, minibatch_size=1, seed=None):
        self.random = np.random.RandomState(seed)
        self.n_hidden = n_hidden
        self.l2 = l2
        self.epochs = epochs
        self.eta = eta
        self.shuffle = shuffle
        self.minibatch_size = minibatch_size
        
    def _onehot(self, y, n_classes):
        onehot = np.zeros((n_classes, y.shape[0]))
        for idx, val in enumerate(y.astype(int)):
            onehot[val, idx] = 1
        return onehot.T
    
    def _sigmoid(self, Z):
        return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
    
    def _forward(self, X):
        # step 1: net input of hidden layer
        z_h = np.dot(X, self.w_h) + self.b_h
        # step 2: activation of hidden layer
        a_h = self._sigmoid(z_h)
        # step 3: net input of output layer
        z_out = np.dot(a_h, self.w_out) + self.b_out
        # step 4: activation output layer
        a_out = self._sigmoid(z_out)
        return z_h, a_h, z_out, a_out
    
    def _compute_cost(self, y_enc, output):
        L2_term = (self.l2 * (np.sum(self.w_h ** 2.) + np.sum(self.w_out ** 2.)))
        term1 = -y_enc * (np.log(output))
        term2 = (1. - y_enc) * np.log(1. - output)
        cost = np.sum(term1 - term2) + L2_term
        return cost
    
    def predict(self, X):
        z_h, a_h, z_out, a_out = self._forward(X)
        y_pred = np.argmax(z_out, axis=1)
        return y_pred
    
    def fit(self, X_train, y_train, X_valid, y_valid):
        n_output = np.unique(y_train).shape[0]
        n_features = X_train.shape[1]
        # weight initialization
        # weights for input -> hidden
        self.b_h = np.zeros(self.n_hidden)
        self.w_h = self.random.normal(loc=0.0, scale=0.1, size=(n_features, self.n_hidden))
        # weights for hidden -> output
        self.b_out = np.zeros(n_output)
        self.w_out = self.random.normal(loc=0.0, scale=0.1, size=(self.n_hidden, n_output))
        epoch_strlen = len(str(self.epochs))
        self.eval_ = {'cost': [], 'train_acc': [], 'valid_acc': []}
        y_train_enc = self._onehot(y_train, n_output)
        
        # iteration over training epochs
        for i in range(self.epochs):
            indices = np.arange(X_train.shape[0])
            if self.shuffle:
                self.random.shuffle(indices)
            for start_idx in range(0, indices.shape[0] - self.minibatch_size + 1, self.minibatch_size):
                batch_idx = indices[start_idx:start_idx + self.minibatch_size]
                z_h, a_h, z_out, a_out = self._forward(X_train[batch_idx])
                # Backpropagation
                sigma_out = a_out - y_train_enc[batch_idx]
                sigmoid_derivative_h = a_h * (1. - a_h)
                sigma_h = (np.dot(sigma_out, self.w_out.T) * sigmoid_derivative_h)
                grad_w_h = np.dot(a_h.T, sigma_out)
                grad_b_out = np.sum(sigma_out, axis=0)
                delta_w_h = (grad_w_h + self.l2*self.w_h)
                delta_b_h = grad_b_h # bias is not regularized
                self.w_h -= self.eta * delta_w_h
                self.b_h -= self.eta * delta_b_h
                delta_w_out = (grad_w_out + self.l2*self.w_out)
                delta_b_out = grad_b_out # bias is not regularized
                self.w_out -= self.eta * delta_w_out
                self.b_out -= self.eta * delta_b_out
            # evaluation
            z_h, a_h, z_out, a_out = self._forward(X_train)
            cost = self._compute_cost(y_enc=y_train_enc, output=a_out)
            y_train_pred = self.predict(X_train)
            y_valid_pred = self.predict(X_valid)
            train_acc = ((np.sum(y_train ==y_train_pred)).astype(np.float) / X_train.shape[0])
            valid_acc = ((np.sum(y_valid == y_valid_pred)).astype(np.float) / X_valid.shape[0])
            sys.stderr.write('\r%0*d/%d | Cost: %.2f ''| Train/Valid Acc.: %.2f%%/%.2f%% ' %
                            (epoch_strlen, i+1, self.epochs, cost, train_acc*100, valid_acc*100))
            sys.stderr.flush()
            self.eval_['cost'].append(cost)
            self.eval_['train_acc'].append(train_acc)
            self.eval_['valid_acc'].append(valid_acc)
        return self

接下来我们初始化一下784-100-10的MLP：

nn = NeuralNetMLP(n_hidden=100, l2=0.01, epochs=200, eta=0.0005,
                 minibatch_size=100, shuffle=True, seed=1)

首先看一下参数的含义：

• l2:：l2正则化系数$ \lambda $
• epochs：遍历训练集的次数（遍历次数）
• eta：学习速率$ \eta $
• shuffle：每次迭代前打乱训练集的数据
• seed：打乱数据和权重初始化的随机种子
• minibatch_size：在每个小批次中训练样本的数目

梯度每个批次分别计算，而不是在整个训练数据集上进行计算，这样做是为了加快学习的速率。

接下来进行训练：

nn.fit(X_train=X_train[:55000], y_train=y_train[:55000],
      X_valid=X_train[55000:], y_valid=y_train[55000:])
>> 200/200 | Cost: 15345.39 | Train/Valid Acc.: 96.10%/96.40% 

我们在上述实现中，我们也定义了eval_用来保存每次迭代后的代价值，我们将其绘制出来：

import matplotlib.pyplot as plt
plt.plot(range(nn.epochs), nn.eval_['cost'])
plt.xlabel('Cost')
plt.ylabel('Epochs')
plt.show()

得到的图像如下：

可以得到前100次cost的值下降得很快，之后随着迭代次数增加，cost值下降不明显。

接下来看一下训练和验证率得变化：

plt.plot(range(nn.epochs), nn.eval_['train_acc'], label='training')
plt.plot(range(nn.epochs), nn.eval_['valid_acc'], label='validation', linestyle='--')
plt.xlabel('Accuracy')
plt.ylabel('Epochs')
plt.legend()
plt.show()

图像如下：

可以发现在迭代次数175之前，拟合模型有点欠拟合。最后我们看一下预测准确率：

y_test_pred = nn.predict(X_test)
acc = (np.sum(y_test == y_test_pred)).astype(np.float) / X_test.shape[0]
print('Acc: %.3f' % acc)
>> Acc: 0.959

可以发现我们的模型在测试集上准确率差不多是96%，在数值上接近训练集中验证的准确率，表明模型拟合程度较好。

最后，看一下一些图片和我们MLP预测结果的示例图：

miscl_img = X_test[y_test != y_test_pred][125:150]
correct_lab = y_test[y_test != y_test_pred][125:150]
miscl_lab = y_test_pred[y_test != y_test_pred][25:50]
fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(25):
    img = miscl_img[i].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys', interpolation='nearest')
    ax[i].set_title('%d) t: %d p: %d' % (i+1, correct_lab[i], miscl_lab[i]))
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

得到的图像如下：

图片上的第二个数字表示的是正确的类标（true class），第三个数字表示的是预测的类标（predicted class）。可以发现，某些图像即便让人工分类也存在一定的困难度。

训练人工神经网络

接下来我们看一下人工神经网络的一些深层的概念，如用于权值更新过程中的逻辑斯蒂代价函数和反向传播算法。

计算逻辑斯蒂代价函数

在_compute_cost方法中实现的逻辑斯蒂代价函数如下：
$$
J(w) = -\sum_{i=1}^{n}y^ilog(a^i)+(1-y^i)log(1-a^i)
$$
其中，$ a^i $是前向传播过程中，用来计算第i个单元的sigmoid激励函数：
$$
a^i = \phi(z^i)
$$
接下来，我们添加一个正则化项，它可以降低过拟合的程度，L2正则化定义如下：
$$
L2：=\lambda ||w||^2_2 = \lambda\sum_{j=1}^{m}w_j^2
$$
通过在逻辑斯蒂代价函数中加入L2正则化项，得到：
$$
J(w) = -\sum_{i=1}^{n}y^ilog(a^i)+(1-y^i)log(1-a^i) =\lambda ||w||^2_2
$$
我们已经实现了一个用于多分类的MLP，它返回一个包含t个元素的输出向量，我们需要将这个输出向量和使用独热编码表示的 $ t \times 1 $维目标向量进行比较。例如，对于一个样本，它在第三层的激励和目标类别（此处是2）可能如下：
$$
a^3 = \begin{bmatrix}
0.1 \
0.9 \
\vdots \
0.3
\end{bmatrix}
,
y = \begin{bmatrix}
0 \
1 \
\vdots \
0
\end{bmatrix}
$$
由此，我们需要逻辑斯蒂函数应用到网络中的所有激励单元j中。因此代价函数（未增加正则化项）：
$$
J(w) = -\sum_{i=1}^{n}\sum_{j=1}^{t}y^i_jlog(a^i_j)+(1-y^i_j)log(1-a^i_j)
$$
这里，上标i表示的是第在训练集中的第i个样本。加入正则化项的公式如下：
$$
J(w) = -\left[\sum_{i=1}^{n}\sum_{j=1}^{t}y^i_jlog(a^i_j)+(1-y^i_j)log(1-a^i_j)\right]

• \frac{\lambda}{2}\sum_{l=1}^{L-1}\sum_{i=1}^{u_l}\sum_{j=1}^{u_l+1}(w_{j,i}^l)^2
  $$
  在这里，$ u_l $表示第$ l $层的数目。我们的目标是最小化$ j(W) $代价函数，因此我们需要计算出网络中各层权重的偏导：
  $$
  \frac{\partial}{\partial{w_{j,i}^l}}J(W)
  $$
  注意$ W $包含多个矩阵，在一个仅仅包含一个隐层单元的MLP中，$ W^h $连接输入层和隐层，$ W^{out} $连接隐层和输出层。下图对$ W $进行可视化：

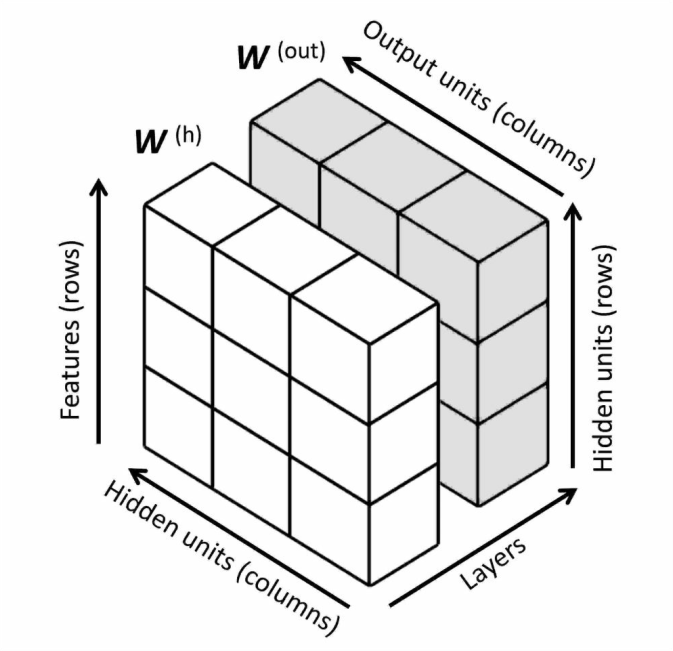
通过反向传播来训练神经网络

回忆本章中介绍的内容，我们需要通过正向传播来获得输出层的激励：
$$
Z^h = A^{in}W^h (隐层的净输入)\
A^h = \phi(Z^h) (隐层的激励)\
Z^{out} = A^hW^{out} (输出层的净输出)\
A^{out} = \phi(Z^{out})(输出层的激励)
$$
简单说，我们按照下图处理输入：

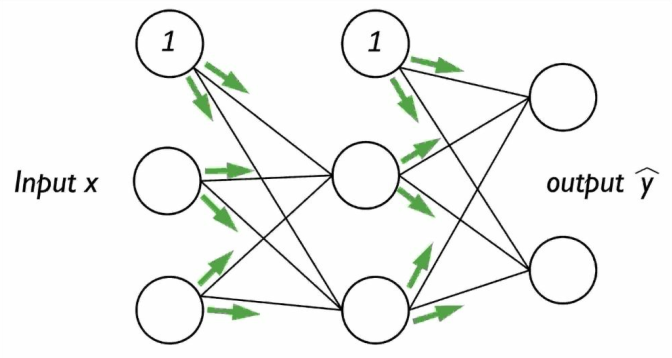
后向传播中，我们将误差从右向左传递。首先计算输出层的误差向量：
$$
\delta^{out} = a^{out} - y
$$
其中，$ y $是真实类标的向量。接下来，我们计算隐层的误差项：
$$
\delta^{h} = \delta^{out}(W^{out})^T \odot \frac{\partial\phi(z^h)}{\partial z^h}
$$
这里，$ \frac{\partial\phi(z^h)}{\partial z^h} $计算公式如下：
$$
\frac{\partial\phi(z^h)}{\partial z^h} = \left(
a^h \odot (1-a^h)
\right)
$$
在这里，$ \odot $表示的是数组元素依次相乘符号。

相应的，$ \delta^h $计算公式如下：
$$
\delta^{h} = \delta^{out}(W^{out})^T \odot \left(
a^h \odot (1-a^h)
\right)
$$
在得到$ \delta $后，我们可以将代价函数的偏导记作：
$$
\frac{\partial}{\partial w_{i, j}^{out}}J(W) = a_j^h\delta_i^{out}\
\frac{\partial}{\partial w_{i, j}^h}J(W) = a_j^{in}\delta_i^h
$$
综上，我们通过下图进行反向传播总结：

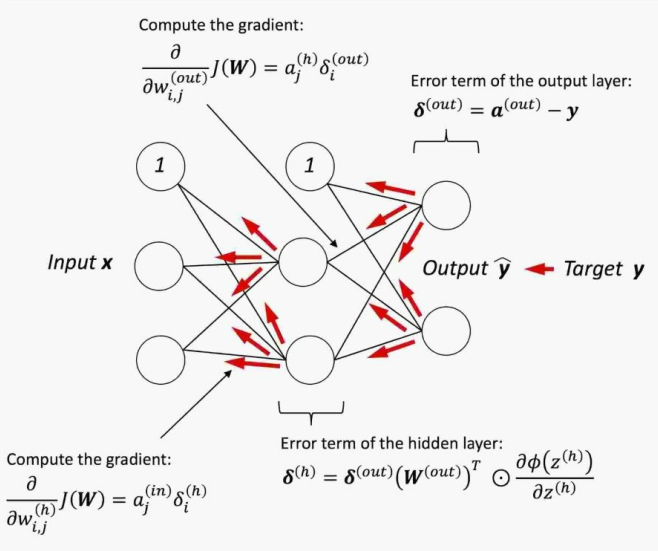
神经网络的收敛性

在前面实现的训练手写数字的神经网络过程中，没有使用传统的梯度下降，而是使用小批次样本学习来替代。随机梯度下降每次仅使用一个样本（k=1）更新权重来进行，虽然这是一种随机的方法，但相较于传统梯度下降，它通常嗯能得到精度极高的训练结果，并且收敛速度更快。子批次学习是随机梯度下降的一个特例：从包含n个样本的训练数据中随机抽取k个用于训练，其中1<k<n。

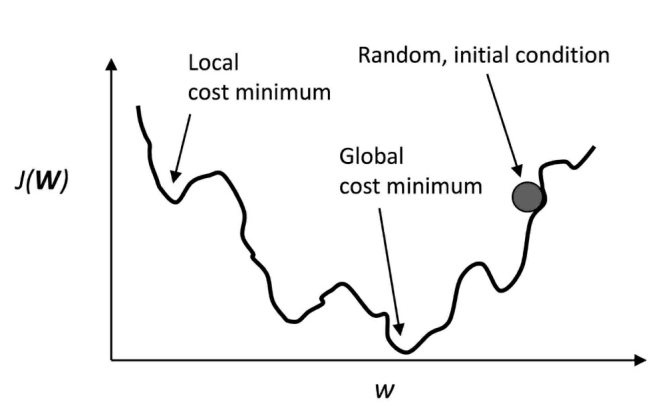
神经网络的输出函数的曲线并不平滑，而且容易陷入局部最优值，如下图：