聚类分析之处理无类标数据

前面几章中，我们使用的数据都是事先已经直到预测结果的，即训练数据中已提供了数据的类标。在本章中，我们转而研究聚类分析，它是一种无监督学习技术，可以在事先不知道正确结果的情况下，发现数据本身所蕴含的结构等信息。

使用k-means算法对相似对象进行分组

本节讨论最流行的聚类算法：k-means算法，它在学术邻域及业界都得到了广泛应用。聚类是一种可以找到相似对象群组的技术，与组间对象相比，组内对象之间具有更高的相似度。

尽管k-means算法适用于高维数据，但出于可视化需要，我们使用一个二维数据集的例子演示：

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=150,
                 n_features=2,
                 centers=3,
                 cluster_std=0.5,
                 shuffle=True,
                 random_state=0)
plt.scatter(X[:, 0], X[:, 1], c='blue', marker='o', s=50)
plt.grid()
plt.show()

图像如下：

k-means算法具体有四个步骤：

1. 从样本点随机选择k个点作为初始簇中心
2. 将每个样本点划分到距离它最近的中心点$ \mu^j, j\in{1,\cdots ,k} $所代表的簇中
3. 用各簇中所有样本的中心点替代原有的中心点
4. 重复步骤2和3，直到中心点不变或者达到预定迭代次数时，算法终止

度量对象之间的相似性可以用欧几里得距离的平方：
$$
d(x, y)^2 = \sum_{j=1}^{m}(x_j-y_j)^2=||x-y||^2_2
$$
基于欧几里得标准，我们可以将k-means算法描述为一个简单的优化问题，也就是使得簇内误差平方和（SSE）最小：
$$
SSE = \sum_{j=1}^n\sum_{j=1}^{k}w^{i,j}=||x^i-\mu^j||_2^2
$$
现在借助scikit-learn中的KMeans类将k-means算法应用于我们的示例数据集：

from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
           init='random',
           n_init=10,
           max_iter=300,
           tol=1e-04,
           random_state=0)
y_km = km.fit_predict(X)

在k-means算法的某次迭代中，可能会发生无法收敛的问题，特别是我们设置了较大的max_iter。解决这个问题的方法是为tol参数设置一个较大的值，上述容忍度为1e-04。

k-means++

我们讨论了经典的k-means算法，它使用随机点作为初始中心点，但是初始中心点选择不当，就会导致收敛速度慢的问题。解决此问题的方法是在数据集上多次运行k-mean算法，并且根据SSE选择性能更好的模型。另外一种方案是使用k-means++算法让初始中心点彼此尽可能远离，相比传统的k-means算法，它能够产生更好的结果。k-means++算法的初始化过程如下：

1. 初始化一个空的集合M，用于存储选定的k个中心点
2. 从输入样本中随机选定第一个中心点$ \mu^j $，并且将其加入到集合M中
3. 对于集合M之外的任一样本点$ x^i $，通过计算找到与其平方距离最小的样本$ d(x^i, M)^2 $
4. 使用加权概率分布$ \frac{d(\mu, M)^2}{\sum_id(x^i, M)^2} $来随机选择下一个中心点$ \mu^p $
5. 重复步骤2，3，直到选定k个中心点
6. 基于选定的中心点执行k-means算法

现在对k-means算法的结果做可视化展示：

plt.scatter(X[y_km==0, 0],
           X[y_km==0, 1],
           s=50,
           c='lightgreen',
           marker='s',
           label='cluster 1')
plt.scatter(X[y_km==1, 0],
           X[y_km==1, 1],
           s=50,
           c='orange',
           marker='o',
           label='cluster 2')
plt.scatter(X[y_km==2, 0],
           X[y_km==2, 1],
           s=50,
           c='lightblue',
           marker='v',
           label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0],
           km.cluster_centers_[:, 1],
           s=250,
           marker='*',
           c='red',
           label='centroids')
plt.legend()
plt.grid()
plt.show()

图像如下：

散点图显示的结果中3个中心点位于各个簇的中心，分组结果看起来是合理的。

k-means算法的一个缺点是我们必须先指定一个簇数量k，但是在实际应用中，簇数量并不总是显而易见的。

硬聚类与软聚类

硬聚类指每个样本只能划至一个簇的算法，如k-means算法；软聚类算法可以将样本划分到一个或多个簇，如FCM算法。

FCM算法和k-means算法十分相似，k-means算法某个样本预测结果是$ [0,1,0] $，表明该样本属于簇2。FCM中可以允许预测的结果中含有分数，如$ [0.7, 0.2, 0.1] $表明该样本属于簇1的概率是0.7，簇2的概率是0.2。FCM的步骤如下：

1. 指定k个中心点，并随机将样本点划分至某个簇
2. 计算各个簇的中心$ \mu^j ,j\in{1, \cdots,k}$
3. 更新各样本点所属簇的成员隶属度
4. 重复步骤2，3，直到各个样本点所属簇成员隶属度不变或者是达到最大的迭代次数

FCM的目标函数如下：
$$
J_m = \sum_{i=1}^{n}\sum_{j=1}^{m}w^m(i,j)||x^i-\mu^j||^2_2
$$

使用肘方法确定簇的最佳数量

簇内误差平方和可以通过inertia访问，基于簇内误差平方和，我们可以使用图形工具，即所谓的肘方法，针对特定任务估计出最优的簇数量k。

distortions = []
for i in range(1, 11):
    km = KMeans(n_clusters=i,
               init='k-means++',
               n_init=10,
               max_iter=300,
               random_state=0)
    km.fit(X)
    distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()

图像如下：

如图，当k=3时团呈现肘形，这表明对于此数据来说，k=3是一个好的选择。

通过轮廓图定量分析聚类质量

另外一种聚类质量的评估方法时轮廓分析，此方法用于k-means算法之外的其他聚类方法。我们通过以下步骤计算轮廓系数：

1. 将某样本$ x^i $与簇内其他点之间的平均距离看作是簇的内聚度$ a^i $

2. 将样本$ x^i $与其最近簇中所有点之间的平均距离看作是与下一最近簇的分离度$ b^i $

3. 轮廓系数如下：
   $$
   s^i = \frac{b^i - a^i}{max{b^i, a^i}}
   $$

可以发现，理想的轮廓系数时1，轮廓系数代码如下：

km = KMeans(n_clusters=3,
           init='k-means++',
           n_init=10,
           max_iter=300,
           tol=1e-04, 
           random_state=0)
y_km = km.fit_predict(X)

import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X,
                                    y_km,
                                    metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper),
                    c_silhouette_vals,
                    height=1.0,
                    edgecolor='none',
                    color=color)
    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg,
            color="red",
            linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()

图像如下：

从上图可见，轮廓系数未接近0点，此指标显示聚类效果不错。为了解聚类效果不佳的轮廓图的形状，我们使用两个中心点来初始化k-means算法：

km = KMeans(n_clusters=2,
           init='k-means++',
           n_init=10,
           max_iter=300,
           tol=1e-04,
           random_state=0)
y_km = km.fit_predict(X)

plt.scatter(X[y_km==0, 0],
           X[y_km==0, 1],
           s=50,
           c='lightgreen',
           marker='s',
           label='cluster 1')
plt.scatter(X[y_km==1, 0],
           X[y_km==1, 1],
           s=50,
           c='orange',
           marker='o',
           label='cluster 2')
plt.scatter(km.cluster_centers_[:, 0],
           km.cluster_centers_[:, 1],
           s=250,
           marker='*',
           c='red',
           label='centroids')
plt.legend()
plt.grid()
plt.show()

图像如下：

接下来，我们绘制轮廓图来对聚类结果进行评估：

cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X,
                                    y_km,
                                    metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper),
                    c_silhouette_vals,
                    height=1.0,
                    edgecolor='none',
                    color=color)
    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg,
            color="red",
            linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.show()

由结果可见，轮廓图由明显不同的长度和宽度，这说明该聚类并非最优结果：

层次聚类

本节中，我们将学习另外一种基于原型的聚类：层次聚类。层次聚类算法的优势在于：他能够使我们绘制出树状图，这有助于我们使用有意义的分类解释聚类结果。层次聚类的另外一个优势在于我们无需指定簇数量。

层次聚类有两种主要方法：凝聚层次聚类和分裂层次聚类。在凝聚层次聚类中，判定簇间距离的两个标准方法分别是单连接和全连接。单连接方法计算每一对簇中最相似两个样本的距离，并且合并距离最近的两个样本所属簇。与之相反，全连接方法是通过比较找到分布于两个簇中最不相似的样本（距离最远的样本），进而完成簇的合并。

本节中，我们主要关注基于全连接方法的凝聚层次聚类，迭代过程如下：

1. 计算得到所有样本间的距离矩阵
2. 将每个数据点看作是一个单独的簇
3. 基于最不相似（距离最远）样本的距离，合并两个最接近的簇
4. 更新相似矩阵
5. 重复步骤2到4，直到所有样本都合并到一个簇为止

计算距离矩阵的方式如下：

import pandas as pd
import numpy as np
np.random.seed(123)
variables = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']
X = np.random.random_sample([5, 3])*10
df = pd.DataFrame(X, columns=variables, index=labels)
df

得到的数据如下：

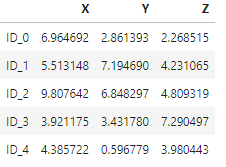
基于距离矩阵进行层次聚类

我们基于SciPy来计算距离矩阵：

from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')), columns=labels, index=labels)
row_dist

得到的数据如下：

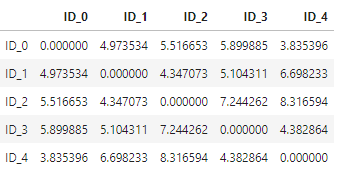
接下来我们使用linkage函数，此函数以全连接作为距离判定标准：

from scipy.cluster.hierarchy import linkage
row_clusters = linkage(df.values, method='complete', metric='euclidean')
pd.DataFrame(row_clusters, columns=['row label 1', 'row label 2', 'distance', 'no. of items'], 
            index=['cluster %d' % (i+1) for i in range(row_clusters.shape[0])])

得到的数据如下：

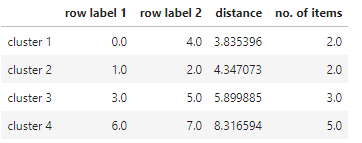
接下来采用树状图的形式对聚类结果进行可视化展示：

from scipy.cluster.hierarchy import dendrogram
row_dendr = dendrogram(row_clusters, labels=labels)
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()

得到的图像如下：

此树状图采用了凝聚层次聚类合并生成不同簇的过程，从图中可见，首先ID_0和ID_4合并，解下来是ID_1和ID_2合并。

树状图与热度图的关联

实际应用中，层次聚类的树状图与热度图结合使用，本节中我们讨论如何将树状图附加到热度图上：

fig = plt.figure(figsize=(8, 8))
axd = fig.add_axes([0.09, 0.1, 0.2, 0.6])
row_dendr = dendrogram(row_clusters, orientation='left')
df_rowclust = df.ix[row_dendr['leaves'][::-1]]
axm = fig.add_axes([0.23, 0.1, 0.6, 0.6])
cax = axm.matshow(df_rowclust, interpolation='nearest', cmap='hot_r')
axd.set_xticks([])
axd.set_yticks([])
for i in axd.spines.values():
    i.set_visible(False)
fig.colorbar(cax)
axm.set_xticklabels([''] + list(df_rowclust.columns))
axm.set_yticklabels([''] + list(df_rowclust.index))
plt.show()

得到图像可得：

通过scikit-learn进行凝聚聚类

本节使用scikit-learn进行基于凝聚的层次聚类：

from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='complete')
labels = ac.fit_predict(X)
print('Cluster labels: %s' % labels)
>> Cluster labels: [0 1 1 0 0]

通过对簇类标的预测结果进行分析，我们可以看出第一第四第五样本被划分至第一个簇，第二第三样本被划分到第二个簇。

使用DBSCAN划分高密度区域

接下来我们介绍另外一种聚类方法：基于密度空间的聚类算法。在DBSCAN中，基于一下标准，每个样本都被赋予了一个特殊的标签：

• 如果一个点周边的指定半径$ \epsilon $内，其他样本点的数量不小于指定数量（MinPts），则此样本点称为核心点（core point）
• 在指定半径$ \epsilon $内，如果一个点的邻居数量小于MinPts时，但是却包含一个核心点，则此点称为边界点（border point）
• 除了核心点和边界点外的其他样本点称为噪声点（noise point）

完成对核心点，边界点和噪声点的标记后，DBSCAN算法可以总结为两个简单的步骤：

1. 基于每个核心点或者一组相连的核心点形成一个单独的簇
2. 将每个边界点划分到对应核心点所在的簇中

为了给出一个更能说明问题的例子，我们创建一个半月形的数据集，以及k-means聚类，层次聚类和DBSCAN聚类进行比较，首先得到半月形数据集：

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.show()

得到的图像如下：

下面首先使用前面讨论过的k-means算法和基于全连接的层次聚类算法，算法如下：

f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km==0,0], X[y_km==0,1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='cluster 1')
ax1.scatter(X[y_km==1,0],
            X[y_km==1,1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='cluster 2')
ax1.set_title('K-means clustering')
ac = AgglomerativeClustering(n_clusters=2,
                            affinity='euclidean',
                            linkage='complete')
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac==0,0],
            X[y_ac==0,1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='cluster 1')
ax2.scatter(X[y_ac==1,0],
            X[y_ac==1,1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='cluster 2')
ax2.set_title('Agglomerative clustering')
plt.legend()
plt.show()

得到的图像如下：

可以发现，上述两个算法无法有效分开两个数组。最后我们试一下DBSCAN算法在此数据集上的效果：

from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2,
            min_samples=5,
            metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db==0,0],
            X[y_db==0,1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='cluster 1')
plt.scatter(X[y_db==1,0],
            X[y_db==1,1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='cluster 2')
plt.legend()
plt.show()

得到的图像如下：

可以发现，DBSCAN算法可以成功地对半月形数据进行划分，这也是DBSCAN算法的优势。