在本节中，我们将会学习主要的数据预处理技术，使用这些技术可以高效地构建好的机器学习模型。

缺失数据的处理

在采集数据的时候，可能有的数据会有缺失的情况。通常我们见到的缺失值是数据表中的空值，或者是类似于NaN的占位符。

首先构造一个含有缺失值的CSV文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd
from io import StringIO

csv_data = """A, B, C, D
1.0, 2.0, 3.0, 4.0
5.0, 6.0, , 8.0
10.0, 11.0, 12.0, 
"""
df = pd.read_csv(StringIO(csv_data))
print(df) 
>>       A     B      C     D
>>  0   1.0   2.0    3.0   4.0
>>  1   5.0   6.0    NaN   8.0
>>  2  10.0  11.0   12.0   NaN

上述代码中，我们通过read_csv将CSV格式的数据读取到pandas库的DataFrame中，可以看到有两个缺失值。

对于大的DataFrame来说，我们可以使用内置的isnull方法来判断某单元中是否含有缺失值：

1
2
3
4
5
6
df.isnull().sum()
>> A    0
>> B    0
>> C    1
>> D    1
>> dtype: int64

通过这个方式我们可以得到每列中缺失值的数量。

将存在缺失值的特征或样本删除

这是最简单的数据处理方式：将含有缺失值的特征（列）或者样本（行）从数据中删除。

可通过 dropna方法来删除包含缺失值的行：

1
2
3
df.dropna()
>>       A     B      C     D
>>  0   1.0   2.0    3.0   4.0

类似地，我们可以通过将axis参数设置为1，以删除包含缺失值的列：

1
2
3
4
5
df.dropna(axis=1)
>>       A     B     
>>  0   1.0   2.0    
>>  1   5.0   6.0    
>>  2  10.0  11.0

同样地， dropna方法还有其他的参数，以应对各种缺失值的情况：

1
2
3
4
5
6
7
8
# only drop rows where all columns are NaN
df.dropna(how='any')

# drop rows that hava not at least 4 non-NaN value
df.dropna(thresh=4)

# only drop rows where NaN in specific columns(here is 'C')
df.dropna(subset=['C'])

删除数据是一种简单的方法，但是如果删除过多的样本，会导致分析结果可靠性不高。接下来学习另外一种最常用的处理缺失数据的方法：插值技术。

缺失数据填充

所谓插值技术是指通过数据集中的其他训练样本的数据来估计缺失值，最常用的插值技术是均值插值（meaneinputation），即使用相应的特征均值来替换缺失值。我们可以使用scikit-learn中的Impute类来实现此方法：

1
2
3
4
5
6
7
8
9
10
from sklearn.preprocessing import Imputer

imr = Imputer(missing_values='NaN', strategy='mean', axis=0)
imr = imr.fit(df)
imputed_data = imr.transform(df.values)
imputed_data
>> array([[ 1. ,  2. ,  3. ,  4. ],
          [ 5. ,  6. ,  7.5,  8. ],
          [10. , 11. , 12. ,  6. ]])

首先计算各个特征列的均值，然后将均值插入到NaN处。参数axis用来控制按列计算均值还是按行计算均值，参数strategy还有median和most_frequent可选值。

理解scikit-learn预估器的API

上一节中，我们使用的Imputer类来填充我们数据集中的缺失值，这个类属于scikit-learn中的转换器类，主要用于数据的转换。这些类中常用的两个方法是fit和transform。其中，fit方法用于对数据集中的参数进行识别并且构建相应的数据补齐模型，而transform方法则使用刚创建的数据补齐模型对数据集中的缺失值进行补齐。

在前面的章节中，我们用到了分类器，它们在scikit-learn中属于预估器类别，其API的设计与转换器非常相似。预估器包含一个predict方法，同时也包含一个transform方法。

处理类别数据

目前我们只学习了处理数值型数据的方法，但是在真实的数据集中，常常会出现类别数据。类别数据可以进一步划分为标称特征和有序特征。有序特征可以理解为类别的值是可以排序的，如T恤的尺寸；相反，标称数据不具备排序的特征，如T恤的颜色。

首先构造一个数据集：

1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd

df = pd.DataFrame([
    ['green', 'M', 10.1, 'class1'],
    ['red', 'L', 13.5, 'class2'],
    ['blue', 'XL', 15.3, 'class1']
])
df.columns = ['color', 'size', 'price', 'classlabel']
df
>>  	color	size	price	classlabel
>> 0	green	M	 	10.1	class1
>> 1	red	    L	    13.5	class2
>> 2	blue	XL		15.3	class1

我们构造的数据包括一个标称特征（颜色），一个有序特征（大小）以及一个数据特征（价格）。类标存储在最后一类。

有序特征的映射

对于有序特征，scikit-learn中没有实现相应的自动转换方法，因此，我们需要手动构造相应的映射。假设尺寸之间的关系是：XL = L + 1 = M + 2.

1
2
3
4
5
6
7
size_mapping = {'XL': 3, 'L': 2, 'M': 1}
df['size'] = df['size'].map(size_mapping)
df
>>  	color	size	price	classlabel
>> 0	green	1	 	10.1	class1
>> 1	red	    2	    13.5	class2
>> 2	blue	3		15.3	class1

如果在后续的过程中需要将整数值还原为有序字符串，可以简单定义一个逆映射字典inv_size_mapping = {v : k for k, v in size_mapping.items()}，然后再使用pandas提供的map方法即可。

类标的编码

许多机器学习库中要求类标以整数值的方式进行编码。需要注意的一点是，类标不是有序的，因此，我们只需要简单的以枚举的方式从0开始设定类标：

1
2
3
4
import numpy as np
class_mapping = {label: idx for idx, label in enumerate(np.unique(df['classlabel']))}
class_mapping
>> {'class1': 0, 'class2': 1}

接下来映射一下就行：

1
2
3
4
5
6
df['classlabel'] = df['classlabel'].map(class_mapping)
df
>>  	color	size	price	classlabel
>> 0	green	1	 	10.1	0
>> 1	red	    2	    13.5	1
>> 2	blue	3		15.3	0

同样可以构造一个逆映射来将类表还原为字符串。

此外，可以使用scikit-learn中的LabelEncoder类可以更加方便完成对类标的编码工作：

1
2
3
4
5
6
from sklearn.preprocessing import LabelEncoder

class_le = LabelEncoder()
y = class_le.fit_transform(df['classlabel'].values)
y
>> array([0, 1, 0], dtype=int64)

同样可以使用inverse_transform方法将类标转换为原始的字符串。

标称特征的独热编码

常见的思路如下，使用LabelEncoder类将字符串转换为整数：

1
2
3
4
5
6
7
X = df[['color', 'size', 'price']].values
color_le = LabelEncoder()
X[:, 0] = color_le.fit_transform(X[:, 0])
X
>> array([[1, 1, 10.1],
       	  [2, 2, 13.5],
          [0, 3, 15.3]], dtype=object)

这样的数据处理是常见的错误处理方式，因为学习算法将会假定green大于blue，red大于green，这显然是不合理的。

标称特征不能像有序特征一样简单赋予一个整数值，最常用的转换方法是独热编码技术。这个方法的思想就是创建一个新的虚拟特征，虚拟特征的每一列各代表标称数据的一个值。在此，我们将color特征转换为三个新的特征：blue，green和red。此时可以通过二进制值来标识样本的颜色。

1
2
3
4
5
6
7
from sklearn.preprocessing import OneHotEncoder

ohe = OneHotEncoder(categorical_features=[0])
ohe.fit_transform(X).toarray()
>> array([[ 0. ,  1. ,  0. ,  1. , 10.1],
          [ 0. ,  0. ,  1. ,  2. , 13.5],
          [ 1. ,  0. ,  0. ,  3. , 15.3]])

另外，我们可以通过pandas中的get_dummies方法，更加方便地实现虚拟特征。

1
2
3
4
5
pd.get_dummies(df[['price', 'color', 'size']])
>> 	price	size	color_blue	color_green	color_red
>>0	10.1	1		0			1			0	
>>1	13.5	2		0			0			1
>>2	15.3	3		1			0			0

将数据集划分为训练数据集和测试数据集

接下来，我们将会使用葡萄酒数据集，可以通过UCI机器学习样本数据库来获得。通过pandas库，我们可以在线获取数据集：

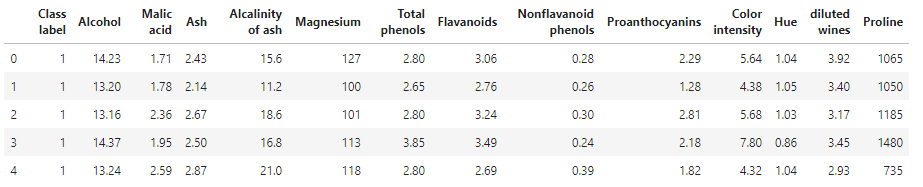
1
2
3
4
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols', 'Flavanoids',
                  'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue', 'diluted wines', 'Proline']
df_wine.head()

得到数据集如下：

1580709518611

葡萄酒样本库通过13个不同的特征，对178个葡萄酒样本划分为类标为1，2，3的三个不同的类别，想要将这些样本划分为训练数据集和测试数据集，可以使用scikit-learn中的train_test_split函数：

1
2
3
4
from sklearn.model_selection import train_test_split

X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

这样，我们就得到了$ 30% $的测试样本和$ 70% $的训练样本。

将特征的值缩放到相同的区间

特征缩放(peature scaling)是数据预处理中至关重要的一步，除了决策树和随机森林不需要特征缩放，其他的机器学习算法几乎都需要这个处理使得算法准确度提高。

特征缩放有两个常用的方法：归一化和标准化。归一化指的是将特征的值缩放到区间$ [0,1] $上，可以使用min-max缩放来实现：
$$
x_{norm}^i = \frac{x^i - x_{min}}{x^i - x_{max}}
$$
在scikit-learn中，已经实现了min-max缩放：

1
2
3
4
5
from sklearn.preprocessing import MinMaxScaler

mms = MinMaxScaler()
X_train_norm = mms.fit_transform(X_train)
X_test_norm = mms.fit_transform(X_test)

而标准化的过程可以使用如下方程：
$$
x_{std}^i = \frac{x^i - \mu_x}{\sigma_x}
$$
其中，$ \mu_x $和$ \sigma_x $分别表示某个特征列的均值和样本。同样地，可以使用scikit-learn中的方法实现标准化：

1
2
3
4
5
from sklearn.preprocessing import StandardScaler

stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.fit_transform(X_test)

选择有意义的特征

如果一个模型在训练数据集上面的表现比在测试数据集上面好很多，那么很可能产生了过拟合。在本节中，我们将会学习使用正则化和特征选择降维这两种常用的减少过拟合问题的方法。

使用L1正则化满足数据稀疏化

在第三章节中，权重向量的L2范数如下：
$$
L2：||w||2^2=\sum{j=1}^{m}w_j^2
$$
而降低模型复杂度的L1正则化公式：
$$
L1：||w||1 = \sum{j=1}^m|w_j|
$$
对于scikit-learn来说，已经支持了 L1的正则化模型，可以将penalty参数设置为’l1’来进行简单的数据稀处理：

1
2
3
from sklearn.linear_model import LogisticRegression

LogisticRegression(penalty='l1')

我们将L1正则化用于标准化处理的葡萄酒数据，经过L1正则化的逻辑斯蒂回归模型可以产生如下稀疏化结果：

1
2
3
4
5
6
lr = LogisticRegression(penalty='l1', C=0.1)
lr.fit(X_train_std, y_train)
print('Training accuracy: ', lr.score(X_train_std, y_train))
print('Test accuracy: ', lr.score(X_test_std, y_test))
>> Training accuracy:  0.9838709677419355
>> Test accuracy:  0.9814814814814815

训练和测试的精确度显示此模型未出现过拟合，通过如下代码可以获得截距项：

1
2
lr.intercept_
>> array([-0.38381104, -0.1580416 , -0.70043119])

由于我们lr对象默认使用了一对多(One vs Rest, OvR)的方法，因此，第一项截距是类别1相对于类别2和类别3的匹配结果。同样，我们可以查看系数矩阵：

1
2
3
4
5
6
7
8
9
10
lr.coef_
>> array([[ 0.2801916 ,  0.        ,  0.        , -0.02793952,  0.        ,
>>         0.        ,  0.71018709,  0.        ,  0.        ,  0.        ,
>>         0.        ,  0.        ,  1.2362193 ],
>>       [-0.64408995, -0.06876656, -0.05722202,  0.        ,  0.        ,
>>         0.        ,  0.        ,  0.        ,  0.        , -0.92643033,
>>         0.06037655,  0.        , -0.37111071],
>>       [ 0.        ,  0.06151885,  0.        ,  0.        ,  0.        ,
>>         0.        , -0.6360538 ,  0.        ,  0.        ,  0.49810762,
>>        -0.35817768, -0.57128442,  0.        ]])

可以发现，权重向量是稀疏的，这意味着只有少数几个特征被考虑进来，符合L1的作用效果。

最后，对L1正则化来说，在强的正则化参数(C<0.1)的作用下，罚项使得所有的特征权重趋于0。

在前面已经介绍过，$ \lambda $是正则化参数，而C是正则化参数的倒数。

序列特征选择算法

另外一种降低模型复杂度从而解决过拟合问题的方法是通过特征选择进行降维，该方法对未经正则化处理的模型特别有效。降维技术主要分为两个大类：特征选择和特征提取。通过特征选择，可以选择原始特征的一个子集；而在特征提取中，通过对现有的特征信息进行推演，构造出一个新的特征子空间。

在本节中，我们着眼于一些经

序列特征选择算法是一种贪婪搜索方法，用于将原始的d维特征空间压缩到一个k维空间中，其中$ k < d $。一个经典的序列特征选择算法是序列后向选择算法（SBS），其目的是在分类行性能衰弱最小的约束小，降低原始数据的维度，提高计算效率。

SBS算法的理念很简单：SBS依次从特征集合中删除某些特征，直到新的特征子空间包含指定数量的特征。为了确定每一步需要删除的特征，为此我们需要定义一个最小化的标准衡量函数J。该函数的计算准则是：比较判定分类器在删除某个特征前后的差异，每次删除的特征，就是那些能够使得标准衡量函数值尽可能大的特征，或者说，每一步特征被删除后，所引起的模型性能损失最小。

基于上述对SBS的定义，总结出以下四个步骤：

  1. 设$ k = d $进行算法初始化，其中 d 是特征空间$ X_d $的维度。
  2. 定义$ x^- $为满足标准$ x^- = argmaxJ(X_k - x) $最大化的特征，其中$ x \in X_k $。
  3. 将特征$ x^- $从特征集中删除：$ X_{k-1} = X_k - x^- , k = k -1$。
  4. 如果k的值等于目标特征数量，算法终止，否则跳转到第2步。

遗憾的是，scikit-learn并没有实现SBS算法，我们可以手动实现它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from sklearn.base import clone
from itertools import combinations
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

class SBS():
    def __init__(self, estimator, k_features, scoring=accuracy_score, test_size=0.25, random_state=1):
        self.scoring = scoring
        self.estimator = clone(estimator)
        self.k_features = k_features
        self.test_size = test_size
        slef.random_state = random_state
        
    def fit(self, X, y):
        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=self.test_size, random_state=self.random_state)
        dim = X_train.shape[1]
        self.indices_ = tuple(range(dim))
        self.subsets_ = [self.indices_]
        score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_)
        self.scores_ = [score]
        while dim > self.k_features:
            scores = []
            subsets = []
            for p in combinations(self.indices_, r=dim-1):
                score = self._calc_score(X_train, y_train, X_test, y_test, p)
                scores.append(score)
                subsets.append(p)
            best = np.argmax(scores)
            self.indices_ = subsets[best]
            self.subsets_.append(self.indices_)
            dim -= 1
            self.scores_.append(scores[best])
        self.k_score_ = self.scores_[-1]
        return self
    
    def transform(self, X):
        return X[:, self.indices_]
    
    def _calc_score(self, X_train, y_train, X_test, y_test, indices):
        self.estimator.fit(X_train[:, indices], y_train)
        y_pred = self.estimator.predict(X_test[:, indices])
        score = self.scoring(y_test, y_pred)
        return score

我们使用k_features来指定需要返回的特征数量，并且最终特征子集的列标被赋值给self.indices_。注意，在fit方法中，我们没有在fit方法中明确地计算评价标准，只是简单的删除了那些没有包含在最优特征子集中的特征。

接下来我们看一下SBS应用于KNN分类器的效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

knn = KNeighborsClassifier(n_neighbors=2)
sbs = SBS(knn, k_features=1)
sbs.fit(X_train_std, y_train)
k_feat = [len(k) for k in sbs.subsets_]
plt.plot(k_feat, sbs.scores_, marker='o')
plt.ylim([0.7, 1.1])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.show()

得到的图像如下：

img

可以发现，当k = {5, 6, 7, 8, 9, 10}时，算法可以达到百分百的准确率。

接下来看一下是哪五个特征在验证数据集上有如此良好的表现：

1
2
3
k5 = list(sbs.subsets_[8])
print(df_wine.columns[1:][k5])
>> Index(['Alcohol', 'Malic acid', 'Alcalinity of ash', 'Hue', 'Proline'], dtype='object')

通过随机森林判定特征的重要性

接下来使用随机森林来从数据集中选择相关特征，下面的代码根据葡萄酒数据集特征重要程度对这13个特征给出重要性等级。但是注意：无需对基于树的模型做标准化或者归一化处理。代码如下：

1
2
3
4
5
6
7
8
from sklearn.ensemble import RandomForestClassifier
feat_labels = df_wine.columns[1:]
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
forest.fit(X_train, y_train)
importances = forest.feature_importances_
indices = np.argsort(importances)[::-1]
for f in range(X_train.shape[1]):
    print("%2d) %-*s %f" % (f + 1, 30, feat_labels[f], importances[indices[f]]))

得到的输出数据如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
 1) Alcohol                        0.182483
 2) Malic acid                     0.158610
 3) Ash                            0.150948
 4) Alcalinity of ash              0.131987
 5) Magnesium                      0.106589
 6) Total phenols                  0.078243
 7) Flavanoids                     0.060718
 8) Nonflavanoid phenols           0.032033
 9) Proanthocyanins                0.025400
10) Color intensity                0.022351
11) Hue                            0.022078
12) diluted wines                  0.014645
13) Proline                        0.013916

从上述输出我们可以得到最具有判别效果的特征是‘Alcohol’。